Truth Table
Truth table is a representation of a logical expression in tabular format. It is mostly used in mathematics and computer science.
The representation is done using two valued logic - 0 or 1. You can also refer to these as True (1) or False (0). It is used to see the output value generated from various combinations of input values.
Logic Gate Symbols
These input values are various variables & symbols ( commonly termed as LOGIC GATES). Below are the GATES and symbols
- AND (symbolically: &)
- OR (symbolically: +)
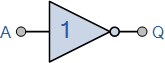
- NOT (symbolically: !)
- NOR (Representing: Not – OR)
- NAND (Representing: Not - AND)
Truth Table Examples
In every truth table, each statement is typically represented by a binary digit or a variable. For better understanding, take a look at below examples.
OR Gate Truth Table
| Symbol |
A |
B |
A+B |
 |
0 |
0 |
0 |
| 0 |
1 |
1 |
| 0 |
1 |
1 |
| 1 |
1 |
1 |
AND Gate Truth Table
| Symbol |
A |
B |
AB |
 |
0 |
0 |
0 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
NAND Gate Truth Table
| Symbol |
A |
B |
!(A.B) |
 |
0 |
0 |
1 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
NOR Gate Truth Table
| Symbol |
A |
B |
!(A+B) |
 |
0 |
0 |
1 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
0 |
NOT Gate Truth Table
| Symbol |
A |
!A |
 |
0 |
1 |
| 1 |
0 |
Truth Table Generator
Truth Table is a mathematical table and the base for all computing needs. It is used to find out if a propositional expression is true for all legitimate input values.
Creating a Truth table involves a simple logic yet sometimes it may slow you down, especially when you are working on a last minute project. This is when you can make use of Truth Table Generator.
Truth Table Generator is an online tool that is used to create logical truth tables instantly. You can enter logical operators in different formats and get accurate results as boolean logic symbols.




